Multipliers

[Last modified 11:12:52 PM on Tuesday, 27 July 2010]
Beating the Optimal Multiplier
This section provides a brief overview of the outcomes of my industrial experience project with Bell Labs Research. A 10x10 bit multiplier had already been previously built, by using 3:2 and 4:2 adder cells in what was considered to be an "optimal" arrangement. My task was to build a multiplier, which could use VHDL generics to allow the multiplication of numbers of any size. The original multiplier was to be used as a benchmark, with the ultimate aim being to match its speed for a 10x10 bit configuration.

A number of architectures were built and analysed, but only the final design is described here. The actual design itself is quite straightforward, however it was the coding style which proved to be an important factor in the synthesis results.

Recursive Adder Tree using GENERATE statements

This design, illustrated in figure 1, is not the one used, but illustrates the concepts used in the chosen architecture.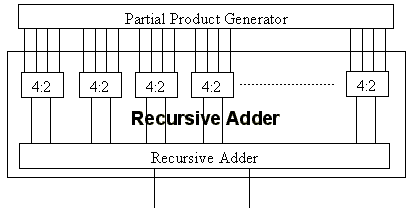


Figure 1 : Architecture of the "recursive" design. Instances of the adder entity may instantiate further instance of the same entity within themselves.
This architecture works by feeding all of the booth recoded partial products and correction terms into a recursive array adder. This adder uses a series of VHDL generate statements to:

• If there are 5 or more inputs to add,
  • Create as many 4:2 compressors as it can
  • Feed any leftovers into another instance of the array adder (with 4 or less inputs)
  • Put all of the results into a new array, which forms the input to another instance of the array adder. Return the results of this new instance.
• Otherwise,
  • If there were 4 inputs, create a 4:2 compressor and return the results
  • If there were 3 inputs, create a 3:2 compressor and return the results
  • If there were 2 inputs, return those inputs as the sum and carry
  • If there was 1 input, return it as the sum, and return a zero carry.

The problem with this technique is that it does not synthesise well, but this can be overcome by alternative methods of coding the same concept.

Adder tree using process statement

This design has a similar approach to the first, but uses a process statement and loops. It takes an array of partial products, and continually reduces them with 4:2 and 3:2 compressors until there are only two left.

The inputs to the top level of adders are the size of the output, containing the partial products shifted to the appropriate columns. The extra bits around the partial product are padded with zeros, and it is left to the synthesiser to remove and optimise these.


Conclusions on multiplier architectures and coding style

It was found that the speed of a synthesised circuit is dependant on not only the architecture chosen, but also the coding style used to implement that design.

In particular, the following conclusions were drawn about the effect of coding style on the performance of a design :

• Process statements synthesise better that "generate"s
• Function calls synthesise better than entity instantiations
• From a synthesis viewpoint, it seems to be better to write code in more small steps rather than fewer complex steps
• It seems to be better to write wasteful code and let Cadence optimise it, rather than to write it efficiently yourself. For example, the described designs use large array containing cells that are either never used, or forced to a constant value. The original design was hand-coded bit-by-bit, so that all operations were performed with no wasted or extra variables.

One of main time saving techniques used in the fastest designs is the use of carry-save adders to combine the partial products into a final answer. The ability of these to combine three or four numbers to two, in a time that is independent of the width of the numbers, is a much more efficient alternative than using traditional adder. Using these, a carry propagate is only required for the final addition of the adder tree.

These observations have been followed when incorporating the multipliers into complex multipliers, which in turn form the basis for the matrix multipliers, and ultimately the signal processor.


Alternative Algorithms

Several possible architectures were considered and built, and the following are two of the more interesting of the alternative ideas:

• [1] describes the use of the redundant binary number system for multiplication. This number system uses three values for each "bit", being 1, 0, and -1, so that additions may be carried out without propagation delay. However, traditionally, this technique still requires a carry-propagation in the conversion from RB to normal binary. This paper claims to have a technique to overcome this, but analysis and experimentation have been unable to verify this claim
  
  
• [2] uses the concept of Left-to-right multipliers to improve the speed of the multiplier. The concept is that the most significant bits of the answer are known before the lesser significant bits, so it is possible to "guess" two alternatives for what the top half should be. The bottom half is created as normal, with a carry-propagate addition, and the carry-out is used to select which of the two alternatives is to be used. This technique did not prove to be as fast, and does not offer carry-save outputs.

References

• [1]Yun Kim, Bang-Sup Song, John Grosspietsch, Steven F. Gillig, "A carry-free 54b x 54b Multiplier Using Equivalent Bit Conversion Algorithm", IEEE Journal of Solid State Circuits, Vol 36, No. 10, October 2001, pp1538
  
  
• [2] Ravi K. Kolagotla, Hosahalli R. Srinivas, Geoffrey F. Burns, "VLSI Implementation of a 200-MHz 16x16 Left-to-Right Carry-Free Multiplier in 0.35mm CMOS Technology for next-generation DSPs", Proceedings of the IEEE Custom Integrated Circuits Conference, 1997, pp469-472