Complex Number Multipliers

[Last modified 11:12:05 PM on Tuesday, 27 July 2010] Once an efficient design for a multiplier had been designed, it could then be extended to multiply complex numbers. However, since complex numbers consist of two components, multiplication is more involved. [See web references for links about complex numbers]

A typical complex multiplication is (a + ib)(c + id), but to perform this calculation in hardware we need to separate the two components:

             (a + ib)(c + id) = (ac - bd) + i(bc + ad)

This means that four separate multiplications are required in total. By observing that the multiplications can be arranged so that "a" and "b" are always the multipliers, and "c" and "d" are always the multiplicands, we can make some savings in logic. This means that only two, not four, booth recoder sections are required, as shown in figure 1.


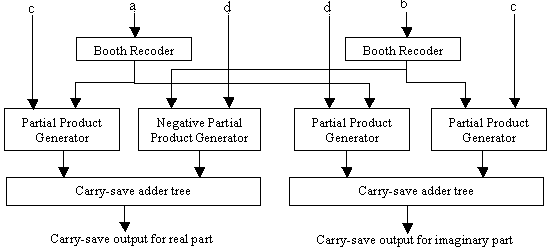
Figure 1: Architecture for a complex multiplier circuit, based on the components of the original multiplier. In addition, it is only necessary to have one adder tree for each component of the output. The only inconsistent part of the design is dealing with the subtraction of the "bd" term, but this can easily be handled by inverting the NEG booth recoded input to the partial product generator.

A further complication is that sometimes, in this particular project, it is necessary to multiply by the conjugate of the value that is read from the inputs. Explicitly taking the conjugate of those values would involve the problem of having to add "1" to the result, especially when we may need to do so again after the booth recoding. Instead, I found it was easier to incorporate this feature into the multiplier, after observing the output of such a calculation:

           (a + ib)(c - id) = (ac + bd) + i(bc - ad)

All that is required is to invert the NEG signal for the bd and ad partial products.


Alternative Approaches
There have been numerous designs for complex multiplication algorithms. Two particular approaches of interest are:

• [1] shows how some of the results can be reused to prevent redundant calculations. For (a+ib)(c+id), the real part of the answer is ac - bd. The imaginary part is bc + ad, but can also be expressed as (a + b)(c + d) - ac - bd. This requires one less multiplication, and three more additions. The algorithm involves using lookup tables and full adders to generate the result, but this technique was not feasible for this project.
  
  
• The use of the redundant binary number system for complex numbers is described in [2]. This number system involves the use of three possible values for each "bit", being -1, 0 and 1, to allow for more efficient arithmetic operations. Previous experience with this number system, for the previous multiplier project, did not make this a suitable candidate.

The most appropriate design was the previously described method of using carry-save adder trees. Unlike the above methods, this technique allows data values to be kept in carry-save format, and manipulated in that form, until the normal binary form is required. This proves particularly useful for matrix multiplication, because the results for an output cell of a matrix consist of the addition of several separate multiplications. In these cases, we only need to know the value of total sum, and not the individual multiplications, so there is no need to convert the multiplication results out of carry-save form.

References

• [1] Y. B. Mahdy, S. A. Ali, K. M. Shaaban, "Algorithm and Two Efficient Implementations for Complex Multiplier",Proceedings of ICECS '99, vol 2, 1999, pp949-952
  
  
• [2] Kyung-Wook Shin; Bang-Sup Song, "A complex multiplier architecture based on redundant binary arithmetic", Proceedings of 1997 IEEE International Symposium on Circuits and Systems. Circuits and Systems in the Information Age. ISCAS 97, pp 1944-1947.