Hermitian Matrix Multiplication

[Last modified 11:12:37 PM on Tuesday, 27 July 2010]
Links to background knowledge on the mathematical theory are available on the links page.

Taking Advantage of Hermitian Matrices

If the input matrices are Hermitian, then they will be of the following form:
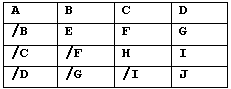
Figure 1 : Form of the 4x4 Hermitian matrix. "/B" means "conjugate of B" The key observation is that for any row n, the corresponding column n contains the conjugates of the same values. The diagonal contains entirely real numbers, which are conjugates of themselves.

In addition, the complex multiplier has already been designed to allow multiplication by the conjugate of its inputs, to cater for the calculation of A*A^*. This provides the necessary components to implement the following simple solution:

• Implement all matrices by storing them in the form of one column within each memory address.
• When a column is needed, simply read the appropriate address
• When a row is needed, read the address of the corresponding column, and set the multiplier to use the conjugate of its input value.

This solution further simplifies the hardware implementation due to the fact that every matrix multiplication requires the reading of rows from one of the matrices. Therefore, the multipliers will always be taking the conjugate of one of the inputs, and the signal that controls this function will be constantly asserted. The synthesis tool will recognise this, and optimise the circuit to remove the redundant case.

Performing multiplications with Hermitian optimisations

One technique is, when we calculate any non-diagonal cell of the output matrix, the conjugate value is also written to its corresponding cell on the other side of the diagonal. Therefore, once the first row of the output matrix has been calculated, the first column has also been assigned new values. The next cell to be calculated is then in the second row and the second column. This pattern continues, and the output matrix is completed in the manner depicted by figure 2.
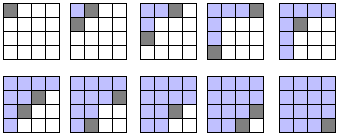
Figure 2 : Order in which the Hermitian matrices are filled in. Dark squares represent the cells currently being written, and light squares represent the cells already calculated. This information is helpful for performing the squaring of Hermitian matrices. Since the rows and columns come from the same matrix, it may first appear that it is necessary to perform two reads per output cell. However, on closer inspection, that is not necessary.

The key observation in figure 2 is that the first cell to be explicitly written on each row of the output matrix lies on the diagonal. That means that the row and column required for that calculation have the same memory address. For the matrix squaring, that means that the first location read for each output row contains both the data for the row to be read, and the column required for the first calculation. All that is required is to store that row's data, and read each column for the other output cells in that row, as required.

For normal matrix multiplications, exactly the same technique can be used. Although it is not necessary to remember the row data in this case, it is more consistent to do so and allows for simpler circuitry.

Multiplication of any Hermitian matrices

The technique described in this section allows for the calculation of any of the previous cases of normal matrix multiplication, in 16 cycles, when all of the source matrices are known to be Hermitian. When one, or none of the source matrices are Hermitian, then the techniques described for generic matrices may be used. Hence, we now have a way for multiplication of almost any combination of valid matrices, so the next step was to build the signal processor that demonstrated an implementation of this theory.