Matrix Multipliers

[Last modified 11:12:48 PM on Tuesday, 27 July 2010] The second major stage to the implementation part of the project was to investigate possible methods for performing matrix multiplications. The approaches can be categorised into three groupings:

• Fully parallel : all multiplications are performed simultaneously
• Fully sequential : There is only one hardware multiplier, and all the multiplications are performed one at a time
• Semi parallel/semi sequential : There are a number of multipliers, so several calculations can be done at once, but several steps are needed to obtain the full result

Each of the first two cases has a major disadvantage that prevents it being suitable for use within the signal processor. The parallel architecture requires excessive surface area in order to implement the required amount of the multipliers. The sequential design is efficient in terms of surface area, but is too slow for the requirements of the signal processor. Hence, a technique is required that uses a small amount of multipliers, but operates over a small enough number of clock cycles.

The approach that was finally decided upon was based on the fact that most of the matrices in the device are of size 4x4. It was decided to attempt to use four multipliers in such a way that an entire output cell could be calculated at once, as is described by figure 1.


Figure 1 : Architecture of a cell generator entity for the parallel multiplication of the values that contribute to its value.

Optimising the Memory Configuration
In order to perform the four multiplications simultaneously, the appropriate row and column must first be loaded from each of the source matrices. It is useless to simply try to load values one at a time from each of the memories, because this would still require four read cycles for each output cell, giving the same total of 64 cycles that limits the fully sequential designs.

However, there is no reason why we can read only one value at a time from each memory. In fact, for the calculation C=AB, the following technique allows the entire row of a 4x4 matrix, A, to be read in one clock cycle:

• The memory for A consists of, not 16, but only 4 addressable locations.
• Each location represents one row, and is logically partitioned into the 4 columns
• The write enable pin of the memory is replaced by a write mask, that selects which of the partitions are overwritten in a write operation. Therefore, the whole memory location does not have to have its contents specified at the one time.
• An entire row of A can be read in one operation
• An single cell of A can be written in one operation, without affecting the other cells in that row.

Figure 2 : Configuration for a memory containing a 4x4 matrix A with 8 bits in each cell. Each memory location contains one row of data, but individual cells can be written by placing a write mask on the separate partitions.
A similar approach can be made for matrix B, by storing the locations in groups of columns instead of rows.

Simple Implementation

With these memory optimizations, it is possible the create a multiplier of two 4x4 matrices that takes only 16 clock cycles, plus the additional cycles required to clear the pipeline. For the operation C=AB, the pipeline stages are

1. Read a row from A, and a column from B
2. Delay so that data has time to arrive from the latched memory outputs
3. Perform the multiplications
4. Tally the multiplication outputs into two carry-save results
5. Resolve the carry-save results into a standard binary form
6. Output result to memory

As with the sequential design, if C is the same as A or B, then the appropriate row or column may be latched when it is first read.

Double Buffering Issues

One of the issues that has needed addressing in this project is the situation when the memory which provides the input matrix is also the destination for the output matrix, such as the calculation A = B*A. A simple approach is to simply use a double buffering approach where we use a different memory for the output, effectively creating two different versions of A.

The double buffering technique may not always be a desirable approach:

• The additional memory requires surface area on the silicon chip
• In an implementation where the same matrix was used several times, logic would be required to keep track of which version of A is the current one, and multiplexers would be required to switch between the two.

By studying the ordering in which values are read and written, we can devise an alternative approach. Considering the calculation C = AB,

• For each cell of C, we need to
  • Read a row of cells from A
  • Read a column of cells from B
  • The most efficient method of generating C is to calculate each cell one at a time, either working across the rows one at a time, or down the columns one at a time
  • For each cell in a given column of C, we require the same column from B. That column from B is not required for calculation of cells in any other column of C.
  • For each cell in a given row of C, we require the same row from A. That row from A is not required for calculation of cells in any other row of C.

Therefore,

• Once we have generated any given column of C, we no longer need the corresponding column from B.
• Once we have generated any given row of C, we no longer need the corresponding row from A.

The solution to the problem is then

• If C and A are the same, then for every row of C,
  • Read in the appropriate row of A for the first cell in that row of C
  • Latch it, and use the latched value for all other cells in that row of C
  • The values that are output will go to the row of C/A that is latched, so the original values can still be used for the time that they are needed.
• If C and B are the same, then for every column of C,
  • Read in the appropriate column of B for the first cell in that column of C
  • Latch it, and use the latched value for all other cells in that column of C
  • The values that are output will go to the column of C/B that is latched, so the original values can still be used for the time that they are needed.

However, only one of these solutions can be used at one time.

Non-conforming matrices
If the memory locations representing the matrix B, in C=AB, do not contain columns of data, then the data can be read as such:

• For each column of output cells,
  • Read each cell for the appropriate column in B, simultaneously reading one of the rows of A (4 read cycles)
  • Store the column that has been read and perform the multiplications as normal
  • Read each of the other three rows and perform the calculations for the respective cells of C (3 read cycles)

This technique requires only 7 reads per output column, giving a total of 7*4 columns=28 cycles for the operation, plus the time required to clear the pipeline.

One matrix doesn't conform, and the other needs to be overwritten

One problem which arose with the original design was an equation of the form B = AB, where both A and B needed to be stored in memory cells containing columns. It is wasteful to simply store the answer in a different memory, and this can further complicate other parts of the design.

• For the problem of reading and writing the same matrix in the sequential design, we would simply store the current column from B while we used its contents and overwrote those values in the memory. We would write B by working down the columns, remembering the column input from B and reading cells from each row of A as required
• For the problem of matrix A not conforming to containing a complete row in one memory location, we decided to read in the row from A, and store it in a latch so that we would not have to repeat those four read operations. We would then work across the rows of the output matrix

Clearly there is a major clash in these two solutions - we cannot calculate the output matrix by working across both the rows and the columns at the same time!

The most critical problem with B = AB is that the output is the same as one of its inputs, so this must be addressed first. The issue of the cells of A being grouped in columns instead of rows requires additional read cycles, but does not affect the output. The solution is then:

• Read the four locations in order to obtain the require row of A. At an appropriate time, read in the column from B that is to be overwritten, and also read in the same column from A (4 read cycles)
• Perform the multiplications as normal for that cell
• For the other cells in the same column of the output matrix, use the stored column of B. For A, we have also stored one column, so we already know one value from the next row. Read the other columns in order to obtain the rest of the row (three reads)
• After each set of 3 reads, perform the calculations as normal

This gives a total of 4+3*3=13 read cycles for each column of the output matrix, with a total of 52 cycles to perform the entire operation. The time required is 1.85 times more than the 28 cycles that would be needed by doing the following, if space permitted:

• using an extra memory to eliminate the problem of reading and writing to the same memory
• using the previously described solution to handle the fact that the contents of A are stored in columns instead of rows.

Squaring Matrices

A further problem is that fact that some of the multiplications that are required involve the same matrix on both inputs. While the solutions above ensure that we can work around the problem of the matrix not conforming to both the row and columns format, it cannot deal with the problem of needing to read two different memory addresses at the same time. One simple approach may be to insert an extra read cycle into the pipeline, but it may not always be desirable to increases the pipeline length in this way. Fortunately, even in the absence of dual read port memories, there exists a solution that does not require additional clock cycles.

As an example, take the 4x4 matrix A, which is stored with an entire column in each memory location. To perform the calculation of one output cell, we need to read an entire row and an entire column:
Figure 3 : The row and column required for the calculation of a given output cell However, since that row and column are sourced from the same matrix, they overlap by one cell:
Figure 4 : The row and column required from a single matrix that is to be squared, required to calculate the output cell. The required row can be read one cell at a time. However, since we actually need to read the whole column in order to obtain that value, at some stage the entire column that is required will also be read. In this way, we can obtain the column "for free", the same as if it had been read from a separate memory.
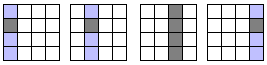
Figure 5 : If the matrix of figure 5-4 is stored so that each address contains an entire column, then to read the row we need to read each column at a time and extract the relevant data for the row. One of these reads will also allow us to obtain the required column "for free". Further optimizations may also be obtained by storing a row or column to prevent the need to reread data, as described above. The result is a squaring operation that can be performed in the same amount of time as an equivalent two matrix multiplication.

Multiplying any combination of matrices

In summary, this page has described methods that would allow the multiplication of any combination of matrices, as described by table 1. In all cases, the sources are 4x4 matrices, but these methods could easily be adapted for any size, and not just square matrices. This assumes that the matrices are stored with either entire rows, or entire columns, in each memory address.

Calculation	Cycles	Comments
C = AB	16	A is stored with rows in each memory address, B with columns in each memory address
C = AB	28	Both A and B are stored with rows in each memory address, or with columns in each memory address.
B = AB	52	A and B are both stored with columns in each memory address. The same method can be adapted for rows, by latching the columns one cell at a time
A = AB	52	Same as B=AB, but the output is calculated by working across the rows, rather than down the columns.
B = A2	52	A is stored with columns in each memory address, but the same method can be adapted for if A contained rows in each address.
A = A2		Not possible. The described method, for when the destination is also one of the sources, is that we calculate the answer by working across either rows or columns of the output, while remembering the corresponding contents of the original. Since squaring requires both rows and columns, this cannot be done unless we use the form B = A2.

Table 1 : Multiplications for 4x4 matrices can be done for almost any configuration. Where a letter A or B appears twice in a single calculation, it is referring to the same matrix.